Рисунки Аксиомы Планиметрии
Сформулируйте содержание аксиом А1. Справедливы все аксиомы и теоремы планиметрии.? АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ. Вспомним основные понятия планиметрии (см. Плакат 1) (точка, прямая: обозначение, изображение). Ученики делают запись и рисунок в тетрадь. Геометрия подразделяется на планиметрию. Пояснение к аксиоме А1.
15 ПЛАН-КОНСПЕКТ УРОКА №1 Предмет Геометрия Урок № 1 Тема урока: Стереометрия. Аксиомы стереометрии Тип урока: Урок-лекция Деятельностная цель: ознакомление учащихся с аксиоматическим методом в геометрии, изучение аксиом о взаимном расположении точек, прямых и плоскостей Образовательная цель: введение на уроке понятия плоскости, изучение и применение аксиом при решении задач. Методы, приемы, технологии обучения: Объяснительно-иллюстративный метод обучения Этап урока Действия учителя Деятельность обучающихся УУД Организационный момент. Приветствие обучающихся.
Аксиомы Планиметрии Рисунки
Изучение планиметрии мы начинали с аксиом планиметрии. В этом видеофрагменте мы рассмотрим аксиомы стереометрии, рассмотрим.
Демонстрируют готовность к учебной деятельности Оценивать ситуации взаимодействия в соответствии с правилами поведения и этики (коммуникативные) Мотивационный этап Учитель задает вопрос, что изучает планиметрия.( раздел геометрии, в которой изучаются свойства фигур на плоскости) Зарисуйте геометрические фигуры в планиметрии. Зарисуйте геометрические фигуры в стереометрии. Что изучает стериометрия(раздел геометрии, в которой изучаются свойства фигур в пространстве) Ученики пытаются ответить на заданные вопросы. Из учебника находят что такое стереометрия. Ученики зарисовывают фигуры. Зарисовывают и сопоставляют их с окружающими нас предметами.
Действие смыслообразования (личностные) Повторение Учитель: Основным методом современной математики является аксиоматический метод, и геометрия не исключение, она так же строится с помощью этого метода. Назовите основные геометрические фигуры на плоскости в планиметрии? Вспомним аксиомы планиметрии Ответ: точка и прямая Вспоминают Самооценка соответствия имеющихся знаний и умений заявленным требованиям (регулятивные) Изучение нового материала Рассмотрим теперь аксиоматический метод в стереометрии.
Что же является основными геометрическими понятиями в стереометрии? Стереометрии удовлетворяют все аксиомы планиметрии, но их не достаточно, поэтому рассмотрим новые аксиомы. Рассматривает Теорему это точка, прямая и плоскость Делятся на группы, используя карточки, на которых даны определенные рисунки, и часть формулировок аксиом ученики пытаются сформулировать аксиомы. Поиск и выделение необходимой информации (познавательные) Закрепление Определите по рисунку: Задача №1 А) Какие две прямые не лежат на одной плоскости? Б) Какие три прямые вместе с прямой АА1 лежат на одной плоскости? Задача №2 По рисунку назовите: а) плоскости, в которых лежат прямые КE, MN, DB.
Б) точки пересечения прямой DM с плоскостью ABC, прямой АE с плоскостью DBC. Задачи из учебника Атанасян.№ 1-5№8 Разбирают совместно с учителем у доски. Выполняют задания в тетрадях. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий (познавательные) Домашнее задание Прочитать пункты 2,3, стр. 4 – 7, выучить наизусть аксиомы и следствия из них, №8 (с объяснением ответов), №9. Познавательные (осознанное и произвольное построение речевого высказывания в устной форме). Рефлексия Учитель спрашивает у обучающихся всё ли понятно или нет.
Регулятивные (адекватно воспринимать оценку учителя). ПЛАН-КОНСПЕКТ УРОКА №2 Предмет Геометрия Урок № 2 Тема урока: Следствия из аксиом стереометрии. Решение задач на применение аксиом. Тип урока: Урок-решения «ключевых задач» Деятельностная цель: ознакомление учащихся с новыми методами решения задач. Образовательная цель: закрепление умений, навыков применять изученные теоретические знания: аксиом стереометрии Методы, приемы, технологии обучения: эвристический метод Этап урока Действия учителя Деятельность обучающихся УУД Организационный момент. Приветствие учителя. Проверка домашнего задания.
Демонстрируют готовность к учебной деятельности. Оценивать ситуации взаимодействия в соответствии с правилами поведения и этики (коммуникативные) Мотивационный этап Учитель раздает карточки, где указано начало аксиом их необходимо продолжить. Ученики заполняют и затем обмениваются карточками и оценивают друг друга. Самооценка соответствия имеющихся знаний и умений заявленным требованиям (регулятивные) Закрепление Для закрепления теорем и аксиом решается задача № 14 из Л.С. Три прямые проходят через одну точку. Через каждые две из них проведена плоскость.
Сколько всего проведено плоскостей? Рассмотрим задачи №7, № 10 а) из учебника Л.С.Атанасян 7. Две прямые пересекаются в точке М.
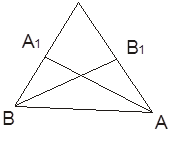
Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости. Лежат ли в одной плоскости все прямые, проходящие через точку М?
Верно ли, что прямая лежит в плоскости данного треугольника, если она: а) пересекает две стороны треугольника Используя задачу № 13 составить обратную задачу 13.Могут ли две плоскости иметь: а) только одну общую точку; б) только две общие точки; в) только одну общую прямую? Решая задачу №7, № 10 а) из учебника Л.С.Атанасян ученики приходят к выводу, что они аналогичные. Используя задачу № 13 создают аналогичную. Решают задачи по вариантам, обосновывают решение. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий (познавательные) Самостоятельная работа Вариант 1 1.Как называется раздел геометрии, изучающий фигуры в пространстве?
2.Назовите основные фигуры в пространстве. 3.Сформулируйте аксиому 2. 4.Сформулируйте аксиому 3. 5.Могут ли прямая и плоскость иметь две общие точки?
6.Сколько плоскостей можно провести через три точки? 7.Сформулируйте любую аксиому планиметрии. Вариант 2 1.Как называется раздел геометрии изучающий фигуры на плоскости? 2.Назовите основные фигуры на плоскости. 3.Сформулируйте аксиому 1 4.Сколько плоскостей можно провести через прямую и не лежащую на ней точку? 5.Сколько может быть общих точек у прямой и плоскости?
6.Могут ли прямая и плоскость иметь одну общую плоскость? 7.Сформулируйте любую аксиому планиметрии. Рефлексия Раздаются карточки с оценками каждый должен оценить себя сам Ученики оценивают от 1-5 баллов Рефлексия способов и условий действия (познавательные). Самооценка (личностные). Домашнее задание Домашнее задание. Задача №12.,10,11 Записывают домашнее задание в дневник Познавательные (осознанное и произвольное построение речевого высказывания в устной форме).
ПЛАН-КОНСПЕКТ УРОКА №3 Предмет Геометрия Урок № 3 Тема урока: Аксиомы стереометрии и следствия из них Тип урока: Урок -консультация Деятельностная цель: закрепление учащимися пройденного материала. Образовательная цель: закрепление умений, навыков применять изученные теоретические и практические знания Этап урока Действия учителя Деятельность обучающихся УУД Организационный момент. Проверка домашнего задания.
Демонстрируют готовность к учебной деятельности. Оценивать ситуации взаимодействия в соответствии с правилами поведения и этики (коммуникативные) Повторение Учитель вспоминает задачу №7 которая является ключевой к № 6 7. Две прямые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости.
Лежат ли в одной плоскости все прямые, проходящие через точку М? Формулирует задачу №1. По рисунку 8 назовите: а) плоскости, в которых лежат прямые РЕ, МК, DB, АВ, ЕС; б) точки пересечения прямой DK с плоскостью ABC, прямой СЕ с плоскостью ADB; в) точки, лежащие в плоскостях ADB и DBC; г) прямые, по которым пересекаются плоскости ABC и DCB, ABD и CDA, PDC и ABC. Ученик вызывается к доске решает задачу №7, следующий ученик решает задачу № 1 Поиск и выделение необходимой информации (познавательные) Закрепление Разбираются задачи №6 и №4 6. Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.
По рисунку 9 назовите: а) точки, лежащие в плоскостях DCC и BQC; б) плоскости, в которых лежит прямая АА1 в) точки пересечения прямой МК с плоскостью ABD, прямых DK. И ВР с плоскостью А1В1С1; г) прямые, по которым пересекаются плоскости АА1В1 и ACD, Р1В1С1 и ABC; д) точки пересечения прямых МК и DC, B1С1 и ВР, С1М1 и DC.
Решают задачу по сложности №4 т.к. Используется новый метод (метод от противного) 4. Точки А, В, С и D не лежат в одной плоскости, а) Могут ли какие-то три из них лежать на одной прямой? Б) Могут ли прямые АВ и CD пересекаться?
Рисунки Аксиом Планиметрии
Ответ обоснуйте. Включается дополнительная задача Решается задача № 15,14 Ученики формулируют вопросы, которые затруднили решение данных задач, используя решенные задачи на доске ученики решают и отвечают на вопросы которые у них возникли по карточкам. Задачи № 6, №2 являются подобными к задачам №7 и №1 Решают задачи с помощью ученика. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий (познавательные) Рефлексия Раздает лист оценивания - я узнал - у меня вызвали затруднения следующие задачи - я не понял (а) Ученики оценивают сами себя Рефлексия способов и условий действий (познавательные) ПЛАН-КОНСПЕКТ УРОКА №4 Предмет Геометрия Урок № 4 Тема урока: Аксиомы стереометрии и следствия из них Тип урока: Зачетный урок Деятельностная цель: проверка учащимися пройденного материала. Образовательная цель: закрепление умений, навыков применять изученные теоретические и практические знания Ход урока 1) Организационный момент 2) Зачёт Вариант 1 Вариант 2 1 Точка Р лежит на прямой МN. Назовите плоскость,которой принадлежит точка Р.
АВС 2) DBC 3) DAB 4) DAC 2. Каким плоскостям принадлежит точка К? 1) АВС и ABD 2) ABD и BCD 3) ACD и ABD 4) ABC и BCD 3. Выберите верные высказывания: 1) Любые три точки лежат в одной плоскости. 2) Если центр окружности и ее точка лежат в плоскости, то и вся окружность лежит в этой плоскости. 3) Через три точки, лежащих на прямой, проходит только одна плоскость.
4) Через две пересекающихся прямые проходит плоскость, и притом только одна. Ответ: 4. Выберите неверные высказывания: 1) Если три прямые имеют общую точку, то они лежат в одной плоскости.
2) Прямая, пересекающая две стороны треугольника, лежит в плоскости этого треугольника. 3) Две плоскости могут имеет только две общие точки.
4) Три попарно пересекающиеся в разных точках прямые, лежат в одной плоскости. Ответ: 5. Назовите прямую, по которой пересекаются плоскости A1BC и A1AD. 1) DC 2) A1D1 3) D1D 4) D1C 6. Назовите прямую, по которой пересекаются плоскости DCC1 и A1AD.
1) DC 2) A1D1 3) D1D 4) D1C 7 Прямые АВ и CD пересекаются. Через прямую АВ проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью ВСD.
1) АС 2) АB 3) BС 4) ВD 8 Прямые АВ и CD пересекаются. Через точки В и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AСD. 1) АС 2) АB 3) BС 4) ВD 1 Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р. АВС 2) DBC 3) DAB 4) DAC 2.
Каким плоскостям принадлежит точка F? 1) АВС и ACD 2) ABD и BCD 3) ACD и BCD 4) ABC и BCD 3. Выберите верные высказывания: 1) Любые четыре точки лежат в одной плоскости. 2) Через прямую и не лежащую на ней точку проходит только одна плоскость.
3) Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости. 4) Две плоскости могут иметь только одну общую точку. Ответ: 4 Выберите неверные высказывания: 1) Две окружности, имеющие общий центр, лежат в одной плоскости. 2) Прямая, проходящая через вершину треугольника, лежит в плоскости этого треугольника. 3) Три вершины треугольника принадлежат одной плоскости.
4) Через две параллельные прямые проходит плоскость, и притом только одна. Ответ: 5 Назовите прямую, по которой пересекаются плоскости DCC1 и A1BC. 1) DC 2) A1D1 3) D1D 4) D1C 6.Назовите прямую, по которой пересекаются плоскости ABC и C1CB. 1) BC 2) B1C1 3) A1B 4) B1B 7.Прямые АВ и CD пересекаются. Через прямую CD проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью AВС.
1) СD 2) АD 3) BС 4) ВD 8 Прямые АВ и CD пересекаются. Через точки A и D проведена плоскость. Назовите линию пересечения данной плоскости с плоскостью BСD.
1) АС 2) АD 3) BС 4) ВD 15.



